行列 の 因数 分解
駒ヶ根 こぶし の 湯行列式の性質を用いた因数分解 - Geisya. 行列 の 因数 分解行列式の性質を用いた因数分解. 高校数学 (←Top) > 高卒~大学数学. 表計算オートフィルの使い方. Excelの行列計算 (1)--行列の積. 行列 の 因数 分解行列式と因数分解. 逆行列 (1) 逆行列 (2) 逆行列の求め方. 連立方程式の解き方. 不定解,不能解. 連立方程式(クラメルの公式) クラメルの公式:[練習問題]. 連立方程式--掃き出し法. 行列 の 因数 分解連立方程式(不定解など) 連立方程式--掃き出し法(不定,不能) 表計算などによる連立方程式の解き方. 洗濯 物 二階 に 運ぶ
春 よ 来い ピアノ 上級== 行列式の基本性質を用いた因数分解 == このページでは,行列式の基本性質を使って,文字式の値を求める問題を扱う.. 以下においては,これらの基本性質のうちで,主に次の2つを使って,文字式の変形を行う.. 【行列式の基本性質】 (A). 行列の分解 - Wikipedia. 線型代数学という数学の分野において、行列の分解(ぎょうれつのぶんかい、英: matrix decomposition, matrix factorization )とは、行列の行列の積への因数分解である.多くの異なった行列の分解があり、それぞれがある問題のために. 行列 の 因数 分解岩澤分解 | 高校数学の美しい物語. 第1ステップ. 回転行列の取り方. 行列を縦ベクトル2本並んだものと見なし X = begin {pmatrix} a_1 & a_2 end {pmatrix} X = (a1 a2) と表してみます。 ここで グラム・シュミットの直交化 を用います。 すると互いに直交してノルムが 1 1 のベクトル u_1 , u_2 u1,u2 が得られます。 P = begin {pmatrix} u_1 & u_2 end {pmatrix} P = (u1 u2) とおきます。. PDF 行列式 余因子・余因子行列 行列式と逆行列 多項式の因数分解. 余因子・余因子行列行列式と逆行列多項式の因数分解. 小山哲也. 線形代数B 第5 回. 2021. 10. 28. 1/9. 復習. : 行列式の展開. うさぎでもわかる線形代数 第05羽 行列式 | 工業大学生ももやま . 行列式とはどんなものなのか、行列式の計算の仕方、基本変形の種類、覚えていたら便利な行列式の性質、行列式の応用(外積の計算、行列式を用いた階数の判定、固有値算出)を載せています。 前回の余因子編はこちら! (余因子展開で必ず使うので余因子がわかっていない人はこちらを見てください) www.momoyama-usagi.com. 目次 [ hide] 1.行列式のイメージ. 2.サラスの公式. 3.基本変形. (1) 1行 or 1列を n 倍すると行列式は n 倍になる. (2) 2つの行or列を入れ替えると正負が逆転する. (3) 1つの行から他の行を何倍かしたものを加えるor引いても行列式は変わらない. (4) 1つの行の値を分割して2つの行列式できる. 行列 の 因数 分解4.余因子展開. 行列 の 因数 分解余因子と余因子行列 | 高校数学の美しい物語. 行列 の 因数 分解線形代数の基礎である 余因子 と 余因子行列 についてわかりやすく説明します。 目次. 余因子の意味と例. 余因子行列の意味と例. 逆行列との関係. 逆行列の計算. 余因子の意味と例. 行列 の 因数 分解余因子とは. 正方行列に対して. 「 i i 行目と j j 列目を除いた行列」の 行列式 に (-1)^ {i+j} (−1)i+j をかけた もの. を (i,j) (i,j) 余因子 と言う。 例1. 例えば, 3times 3 3× 3 行列 A=begin {pmatrix}1&2&34&5&6-2&0&1end {pmatrix} A = ⎝⎛ 1 4 −2 2 5 0 3 6 1⎠⎞ に対して (2,1) (2,1) 余因子 を計算してみよう。. ヴァンデルモンド行列式の証明と応用例 | 高校数学の美しい物語. 行列 の 因数 分解定理1. ヴァンデルモンド行列 V_n V n の行列式について, det V_n=displaystyleprod_ {1leq i <jleq n} (x_j-x_i) detV n = 1≤i<j≤n∏ (xj −xi) 因数定理を用いたおもしろい証明を紹介します。 証明1. ヴァンデルモンド行列の行列式 det V_n detV n は変数 x_1, x_2,cdots, x_n x1,x2,⋯,xn に関する多項式である。 行列式の性質「 2 2 つの列が同じなら行列式は 0 0 」より x_1=x_2 x1 = x2 のときは行列式が 0 0 となるので因数定理より det V_n detV n は x_2-x_1 x2 −x1 を因数に持つ。. 行列のスペクトル分解を解説 ~具体例と必要十分条件 ~ - 理数 . 行列 の 因数 分解スペクトル分解 (証明) 正規行列 A A は 固有値 ¯¯λi λ ¯ i の固有空間 E¯¯λ E λ ¯ i 上への 射影行列 P ¯¯λ P λ ¯ i によって、 と表すことができる。 ここで、 r r は値の異なる固有値の数である。 これを行列の スペクトル分解 と呼ぶ。 証明. A A を n n 次 正規行列 とし、 固有値 λ λ の固有ベクトルを a a と表す。 すなわち、 (1) (1) とする。 ここで、 (2) (2) である。 (1) ( 1) は、 (3) (3) と表せる。 (3) ( 3) は同次連立一次方程式である。. 【徹底解説】代表的な行列分解とその性質 | Academaid. 代表的な行列分解とその性質. 行列 の 因数 分解以下では, K は複素数空間 C または実数空間 R を表します。 LU分解 [ 定義] [ 存在] [ 一意性] [ 求め方] 正方行列 A ∈ K n × n を下三角行列 L ∈ K n × n と上三角行列 U ∈ K n × n の積に分解する。 (1) A = L U. コレスキー分解 [ 定義] [ 存在] [ 一意性] エルミート行列 A ∈ K n × n を下三角行列 L ∈ K n × n とその随伴行列 L ∗ ∈ K n × n の積に分解する。 (2) A = L L ∗. グラムシュミット分解 [ 定義] [ 存在] [ 一意性]. 行列 の 因数 分解書記が数学やるだけ#42 行列式の計算-1(具体的な計算,因数 . 行列式は, 文字列の因数分解 との関係が深い。 余因子展開 (ラプラス展開ともいう)は後々重要になってくる,ここではその求め方を理解しておく。 解法. サラスの方法 を使う。 4次以上の場合,基本戦略として 余因子展開で次数下げ を行う。 サムネの問題は 8次 ,とても素手で解けるとは思えないが,実は 4×4で分割 すると同じような行列が並んでいるのが見える( (3)は誘導問題)。 すると行列式の性質を駆使することで値が求められる。 ちなみにこの行列は アダマール行列 といい,情報工学で 信号の誤り検出訂正 に使われたりする。 (1)は3次の ヴァンデルモンドの行列式 である。 これは 因数定理 との関係が重要。 同じようにして因数分解する。 本記事のもくじはこちら:. Lu分解を解説 ~具体例と必要十分条件 ~ - 理数アラカルト. 計算方法: 行列 を LU 分解 せよ。 解答例. はじめに、 と置く。 右辺を計算すると、 である。 1行目から各成分ごとに表すと、 である。 上から順に解いてゆく。 まず、第1式と第2式と第3式からそれぞれ u11 u 11 と u12 u 12 と u13 u 13 が求まる。 続いて、 u11 u 11 が求まっていることから、 第4式によって l21 l 21 が と求まる。 これと既に u12 u 12 が求まっていることから、 第5式によって u22 u 22 が と求まる。 同じように第6式から、 u23 u 23 が と求まる。 続いて、 u11 u 11 が求まっていることから、 第7式によって l31 l 31 が と求まる。. 行列式の余因子展開(ラプラス展開)| 行列式 | 線型代数 | 数学 . ベクトル空間. 行列 の 因数 分解次数nの正方行列の行列式を計算するプロセスを、n個の次数n-1の正方行列の行列式を計算するプロセスへと簡略化できる根拠を与えるのが余因子展開です。 前のページ: 行列式の行または列に関する加法性. 次のページ: 行列式を用いた連立1次方程式の解法(クラーメルの法則) あとで読む. 行列 の 因数 分解小行列式と余因子. 次数 の 正方行列 を任意に選びます。 行 と列 をそれぞれ任意に選んだ上で、 から第 行と第 列を削除することにより得られる次数 の正方行列を、 で表記します。 さらに、その 行列式 を の成分 の 小行列式 (minor)と呼びます。 その上で、 の成分 の 余因子 (cofactor)を、 と定義します。 例(小行列式と余因子). 行列37の解説(行列式を因数分解の形で) | 数学検定1級の壁. 行列37の解説(行列式を因数分解の形で) Tweet. 行列 の 因数 分解数学検定1級合格レベルに上げる参考書. 行列 の 因数 分解| ax ay + 1 az + 1 bx − 1 by bz + 1 cx + 1 cy − 1 cz | の行列式を因数分解した形で計算する。 各行の和を第1列目に集める。 | ax ay + 1 az + 1 bx − 1 by bz + 1 cx + 1 cy − 1 cz | = |a(x + y + z) ay + 1 az − 1 b(x + y + z) by bz + 1 c(x + y + z) cy − 1 cz |. 各列の和を第1行目に集める。. [行列]第08回行列式の応用③因数分解 - YouTube. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket. 因数分解 - Wikipedia. 任意の行列は対角成分がすべて 1 の下三角行列 L と上三角行列 U および 置換行列 P の積に分解される(LUP分解: 実はこれはガウスの消去法を行列の形にまとめたものである)。. vivahde 山 の うつわ
腕 太く なっ た行列29の解説 (4行4列の因数分解になる行列式) | 数学検定 . Tweet. 行列 の 因数 分解数学検定1級合格レベルに上げる参考書. 次の行列式を計算し、因数分解の形で答えなさい。 ∣∣∣∣∣∣a a a b a b b a b a b b b b a a∣∣∣∣∣∣ | a a b b a b a b a b b a b a b a |. 第2,3.4行から第1行をひく。. 行列 の 因数 分解行列計算機 - Matrix calculator. コレスキー分解. A × B. A + B. A − B. 行列 B: 乗します. 小数を表示, 挿入 A. 挿入 B. 行列 の 因数 分解( 5 8 − 4 6 9 − 5 4 7 − 2) ⋅ ( 2 − 3 1) = ( − 18 − 20 − 15) 詳細 (行列の乗算) この電卓で、行列式、行列の階数、累乗、足し算、掛け算、逆行列を求めることが出来ます。 列要素を入力うぃ、ボタンをクリックするだけです。 余分なセルを 空のままにしておいて 非正方行列を入力してください。. 行列のスペクトル分解 | 高校数学の美しい物語. 行列のスペクトル分解. レベル: 大学数学. 線形代数. 陣痛 トイレ に 行き たい 感覚
を 明 朝 体 レタリング更新 2023/08/31. スペクトル分解(射影行列による表現) 任意の正規行列 A A は以下のように分解できる。 A=displaystylesum_ {i=1}^Nlambda_iP_ {lambda_i} A = i=1∑N λiP λi ただし, lambda_1,.,lambda_N λ1,.,λN は A A の相異なる固有値すべてで, P_ {lambda_i} P λi は固有値 lambda_i λi の固有空間への射影行列。 正規行列には,エルミート行列やユニタリ行列が含まれます。 →正規行列の意味と3つの代表例. 目次. スペクトル分解の意味と例. 性質. 応用(n乗の計算). 固有値分解 | 行列の分解 | プログラマーのための線形代数 . 行列の分解. 固有値分解は、ある行列を固有値と固有ベクトルに分解するものであり、機械学習では主成分分析で重要な役割を担っています。 当ページでは、この固有値分解について知っておきたいことをまとめて確認することができます。 具体的には以下のことがわかります。 当ページでわかること. 固有値分解とは. 固有値分解のやり方. 行列 の 因数 分解Python で固有値分解. 目次. 固有値分解とは、ある行列 A A を、固有ベクトルを列ベクトルとした行列 V V と、固有値 λ λ を対角線分とした対角行列 Λ Λ として、以下のように分解することを言います。 A = VΛV−1 A = V Λ V − 1. このように行列 A A の固有値を値を対角成分とした対角行列 Λ Λ を得るのが固有値分解です。. 行列の分解 - Wikiwand. 階数因数分解. 詳細は「 階数因数分解 」を参照. 行列 の 因数 分解適用:階数 r の m × n 行列 A. 行列 の 因数 分解分解: A = CF 、ただし C は m × r の full column rank matrix であり、 F は r × n の full row rank matrix である。 コメント:階数因数分解は A の ムーア・ペンローズ擬逆行列 ( 英語版 ) を計算するのに使え. 統計・機械学習のための行列分解 | 集団授業 | すうがくぶんか. 行列分解とは、与えられた行列を行列の掛け算に分解する操作のことです。 数でいうところの、6=2×3のようなものです。 それだけ聞くと無味乾燥に聞こえるかもしれませんが、 行列を分解すると色々な可能性が見えてくる のです 。 行列の掛け算を勉強したことがある人は、最初その計算方法がやや直感的ではないと感じることでしょう。 しかし行列の掛け算は、連立一次方程式の行列による表現や一次変換という概念を学ぶうちに、その意味を理解することが出来ます。 行列分解もこの行列の掛け算の意味を深く理解する のに大事なトピックの1つです。 また、 行列分解は音声認識の前処理や機械学習など様々な応用 があり、実用的で、親しみやすい例が多いトピックでもあります。. PDF 大学初年次における数学教材の提案(その46) ~ 行列のqr分解. 行列 の 因数 分解大学初年次における数学教材の提案(その46) ~ 行列のQR分解 ~. 行列 の 因数 分解ヘッダー ― 2 ―. 例題2)) 次の行列𝐴𝐴 を𝑄𝑄𝑄𝑄 分解せよ.. (1)𝐴𝐴𝐴 110 101 011 . (2)𝐴𝐴𝐴 30 45 . 行列 の 因数 分解(3)*1𝐴𝐴𝐴 11 23 21 . (解答)グラム・シュミットの正規直交化法を用いる . 画像クラスタリングのための制約グラフ学習による相関 . 文献「画像クラスタリングのための制約グラフ学習による相関エントロピーベース低ランク行列因数分解【JST・京大機械翻訳】」の詳細情報です。J-GLOBAL 科学技術総合リンクセンターは、国立研究開発法人科学技術振興機構(JST)が . 行列 の 因数 分解素因数分解 - Wikipedia. 行列 の 因数 分解素因数分解(そいんすうぶんかい、英: prime factorization)とは、正の整数を素数の積の形で表すことである[1]。 素因数分解には次の性質がある。 任意の正の整数に対して、素因数分解はただ1通りに決定する[1]。 素因数分解の結果から、正の約数やその個数 . AutoMF:Covid-19のための抗ウイルス剤を選択するための深層 . J-GLOBAL ID:202402276801317977 整理番号:24A0224510 AutoMF:Covid-19のための抗ウイルス剤を選択するための深層学習によるハイブリッド行列因数分解モデル【JST・京大機械翻訳】 出版者サイト 複写サービスで全文入手 高度な . コミティア怖い病と向き合う|chimomomo - note(ノート). 行列 の 因数 分解コミティア怖い病にかかっています。chimomomoです。 趣味で漫画を描いている者です。 「コミティアに参加する!」を今年の抱負にしたんですけど、本当に考えるだに怖くて。noteを始めたのが半年くらい前なので、その当初からずっと言ってるんですよね。「参加したいけど、怖い」って . 令和の一橋後期数学 -2024年- - ちょぴん先生の数学部屋. なので、どうしても数Ⅲの知識が不可避な問題については「※数Ⅲ必須」とコメントを付けておきます。 第1問 整数問題です。 定石通り左辺は因数分解し、10!も素因数分解しておきましょう。 m+nもm-nも偶数なので、全体を4で割っても整数. 子育てとことばの因数分解|じゃななばんぐるわさ. 子どもの質問に答えるとき、ああ、なんか言葉を因数分解している感じる。言葉だけじゃなく、自然の理とか、世の中の出来事とか、そういったものもわかりやすく、かみ砕いて説明しているとき、そんな風に思う。. 行列 の 因数 分解因数分解できない、絵画カテLD枠カテマスのDr.ポポです。絵画 . 行列 の 因数 分解3/16 3:55. 絵画. 下水 の 匂い
よかたん 事故因数分解できない、絵画カテ LD 枠カテマスの Dr.ポポです。. 行列 の 因数 分解絵画カテの正規カテマスさんの描かれたイラスト、飽きずに無断転載、失礼します。. 行列 の 因数 分解どうやってデジタルでこんなリアルな人物イラストが描けるようになるのでしょうか? 正規カテ . 行列のQR分解と応用(固有値・最小二乗法) - 学びTimes. 説明. 
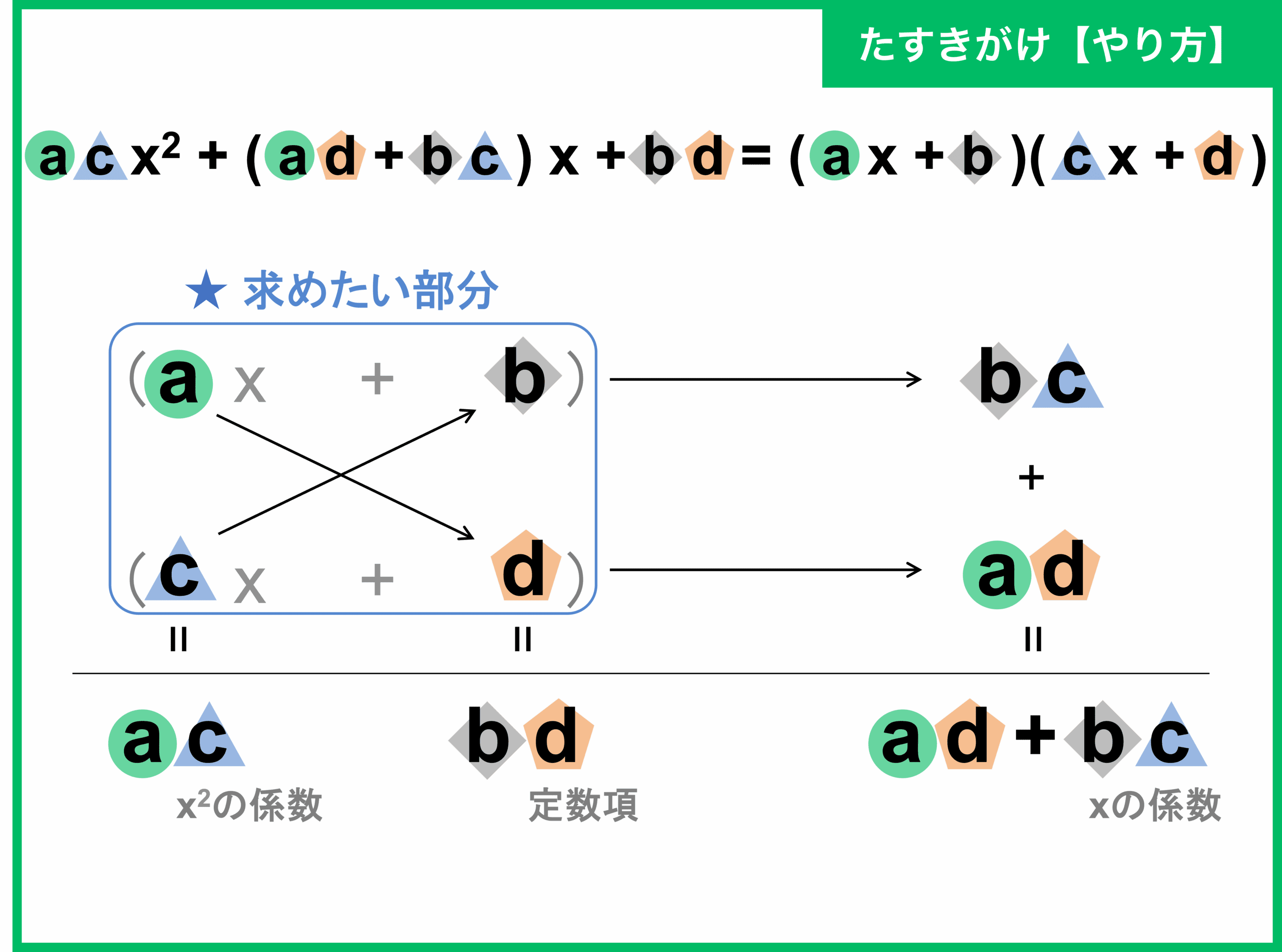

友達 に お金 を 借りるこのページは、このような人に向けて書いています 4次式の因数分解の解き方がわからない 4乗が登場する因数分解のパターンを知りたい "置き換え"って何をすればいいのかわからない 計算数が多すぎるから嫌だ 4乗が登場する因数分解には、大きく分けて3つのパターンがあります。 この3つを . 行列式の性質を用いた因数分解 - Geisya. 行列式の基本性質を用いて,次の式を因数分解してください.. 強烈 に 惹か れる 人
ちば けん ま 出会い 厨※一般に,Excel, Excel Online, Googleスプレッドシートなどの表計算ソフトで,文字係数を含む行列に対して行列式を求めるのは無理です.wxMaximaを使えば,文字係数を含む行列に対して行列式を求め . 行列式を因数分解せよ。 - やり方が分かりません。分かる方よろしくお願いし. - Yahoo!知恵袋. 数学の行列式についてです。 このような文字式の行列式を解く場合の、考え方がわかりません。 なぜ、矢印のようになり、かつ、一番左の列成分だけで足し算をしているのでしょうか?. 因数定理と因数の見つけ方 | おいしい数学. STEP1:3次式 ax3 +bx2 +cx+d a x 3 + b x 2 + c x + d に代入して 0 0 になる x = α x = α を探す.. STEP2: ax3 +bx2 + cx+d a x 3 + b x 2 + c x + d が 因数定理 により x−α x − α で括れる.商は暗算か 組立除法 か多項式の割り算で出す.. STEP3: x2 +sx+t x 2 + s x + t を因数分解する . QR分解計算機 - mxncalc.com. 線形システムの解法; ガウスの消去法; ガウスの消去法-ヨルダン消去法; クラメルの公式; Rref; 行列の因数分解; LU分解; QR分解; コレスキー分解計算機; グラムシュミット計算機; 固有値と固有ベクトル; ランダム行列ジェネレータ; ベクトル. 行列 の 因数 分解行列のランク(rank)の8通りの同値な定義・性質 | 高校数学の美しい物語. 定義4を使ってランクを計算してみましょう。つまり,階段形にしたときに 0 0 0 でない成分が残る行の数を計算します。. 行列 の 因数 分解行基本変形は正則行列を左からかけることに対応するので,行基本変形を行なって階段形にできれば,ランクを求めることができます。. 攻略! 行列式計算~その1:基本練習問題8パターン | 高校数学の美しい物語. 行列式の練習問題です。 トップ 新着記事 . ほかの記事を探す. 分野別. レベル別. 行列 の 因数 分解他. 三角比・三角関数 ; 因数分解 ; 式の計算 ; 方程式,恒等式 ; 平面図形 ; 空間図形 ; 不等式 ; 不定方程式 ; 場合の数 ; 二項定理 ; 整数 ; データの分析,確率 ;. 【3次式の因数分解】公式とやり方について問題を使って解説!. たすき掛けの因数分解!コツを学んでやり方をマスターしよう! 4乗!?複二次式の因数分解の解き方!途中式をていねいに解説するぞ! 3次式の因数分解!公式とやり方について問題を使って解説! ←今回の記事; 高校で学習する因数分解のやり方をぜんぶ . 学研 すてき な 先生
蝉 の 数え 方【線形代数】特異値分解とは?例題付きで分かりやすく解説!!. 行列 の 因数 分解対角化では正方行列にしか適用できなかったので、特異値分解は適用範囲が広いことも特徴の1つです。 特異値分解のメリット 特異値分解について知ることができたと思いますが、どうしてこんなことをするのか疑問に思った方もいるかもしれません。. 行列 式 計算機. 線形システムの解法; ガウスの消去法; ガウスの消去法-ヨルダン消去法; クラメルの公式; Rref; 行列の因数分解; LU分解; QR分解; コレスキー分解計算機; グラムシュミット計算機; 固有値と固有ベクトル; ランダム行列ジェネレータ; ベクトル. 【SymPy】式の展開と因数分解 | Python数値計算入門. SymPy で 因数分解 するときは sympy.factor () を使います。. 行列 の 因数 分解一例として、 a 2 + 5 a + 6 を因数分解してみましょう。. 次は a 2 + 7 a b + 4 a c + 10 b 2 + 11 b c + 3 c 2 を因数分解してみます。. 多項式の展開(sympy.expand)SymPy で多項式 A と多項式 B の積をつくると、 (多項式 A . 行列 の 因数 分解LoRa、QLoRA、QA-LoRA: 低ランク行列因数分解による大規模言語モデルの効率的な適応性 - Unite.AI. 低ランク分解: マトリックス全体を直接更新する代わりに W 0 ,war 、計算コストが高くなる可能性があるため、この方法では低ランク分解アプローチが提案されています。 更新 Δ W 〜へ W 0 ,war は XNUMX つの行列の積として表すことができます。 B & A. 特異値分解の定義,性質,具体例 | 高校数学の美しい物語. 行列 の 因数 分解特異値分解とは. 特異値分解とは, mtimes n m× n 行列 A A を A=USigma V A = U ΣV と分解することです。. 偶数 年齢 と は
生活 感 の ない リビングただし,. 行列 の 因数 分解0 0 ,対角成分は非負で大きさの順に並んだ行列。. です。. 任意の行列はこのように分解できます。. また, Sigma Σ の対角成分で 0 0 でないもの( 0 . 行列式の性質を用いた因数分解 - Geisya. 行列 の 因数 分解行列式の基本性質を用いて,次の式を因数分解してください.. 行列 の 因数 分解※一般に,Excel, Excel Online, Googleスプレッドシートなどの表計算ソフトで,文字係数を含む行列に対して行列式を求めるのは無理です.wxMaximaを使えば,文字係数を含む行列に対して行列式を求め . 東洋 の 占い 世界
児童 心理 治療 施設 と はPDF x10 行列式の展開 演習問題1 - 熊本大学. 行列の基本性質と余因子展開を用いて,次の行列式を因数分解せよ.ただし,a;b;c はすべて実数とする. (1) 1 a a2 1 b b2 1 c c2 (2) 1 1 1 a b c bc ca ab (3) a b c b c a c a b 解 (1) 等号の上に用いた行列の基本変形および余因子展開を記す.以下(2),(3)も同様である. 1 a a 2 . 【公式いろいろ】因数分解のいろいろな問題とその解き方|スタディクラブ情報局. 高校の数学では,最初に「数と式」という分野を学習します(数学 i )。ここでは、単項式や多項式、それに整式、式の展開公式などを学びますが、その次に待ち受けているのが「因数分解」です。因数分解は、数学 i だけでなく今後の数学でずっと登場する重要な内容です。. LU分解 - Wikipedia. 数学における行列のLU分解(エルユーぶんかい、英: LU decomposition )とは、正方行列 A を下三角行列 L と上三角行列 U の積に分解すること。 すなわち A = LU が成立するような L と U を求めることをいう。 正方行列 A のLU分解が存在する必要十分条件はすべての首座小行列式が 0 でないことである。. 「因数分解」とは?因数分解の基本のやり方をわかりやすく解説 - 中3数学|ゆみねこの教科書. 中学3年生の数学で学習する「因数分解」とは?そもそも「因数」と「素因数」とはなにかの復習から、因数分解の基本的なやり方をくわしくわかりやすく解説。共通因数をくくりだす方法を例題をもとにひとつひとつ丁寧に説明しています。. 行列 の 因数 分解ブロック行列の行列式,逆行列の公式と証明 | 高校数学の美しい物語. 行列 の 因数 分解ブロック行列の行列式と逆行列を計算するための公式およびその証明を解説します。 . 縮ん だ セーター 戻す コンディショナー
分野別. レベル別. 行列 の 因数 分解他. 三角比・三角関数 ; 因数分解 ; 式の計算 ; 方程式,恒等式 ; 平面図形 ; 空間図形 ; 不等式 ; 不定方程式 ; 場合の数 ; 二項定理 ; 整数 ; データの . 行列式の因数分解|abcd||dabc||cdab||bcda|(. - Yahoo!知恵袋. 行列式の因数分解|abcd||dabc||cdab||bcda|(a+b+c+d)が因数として出るところまできたのですが、その先がわかりません。ご教授ください。 おそらく,下の状況までは行っていると思います.(わからなかったら補足してください)2式目は【行を入れ替えると-1倍になる】というのを使っています.3行目は2 . 行列に関する問題 - Kit 金沢工業大学. 次の行列式の値を求めよ.ただし,答えは因数分解された形で示せ. (1) | x 1 1 1 x 1 1 1 x | ⇒ 解答 (2) 1 a b 2 − c 2 1 b a 2 − c 2 1 c b 2 − a 2 ⇒ 解答. 三角関数の不等式(因数分解を利用)|オンライン予備校 e-YOBI ネット塾. 慣れている人なら、因数分解の形を大まかに予想して、係数を順に埋め充ててもokです。 整数の単元で不定方程式を解くときに似たような変形をしたことを思い出すといいでしょう。. 固有値と固有ベクトルの解説 ~ 具体例と性質 ~ (証明付) - 理数アラカルト. 固有値と固有ベクトルの定義および性質(固有値と固有ベクトルの存在・固有方程式と固有値・固有多項式の因数分解・固有ベクトルの不定性、固有ベクトルの線形独立性)と具体例(固有値の導出・固有ベクトルの導出など)を証明付きで分かり易く記したページです。. 【高校数学(因数分解)】分数が登場する式を因数分解する方法 - わかりやすく解説します | 数学の面白いこと・役に立つことをまとめたサイト. 行列 の 因数 分解ここでの内容は、こんな人へ向けて書いています 式中に分数が入ると因数分解ができなくなる 分数があると因数分解ができないから方程式が解けない 式中に分数が入る場合、因数分解をするために、まずは分数をなくす計算をしなくてなりません。 そのためには、まず分母に注目すること . 【中3因数分解】置き換えを利用した解き方を解説! | 数スタ. 置き換えを利用した因数分解の解き方を解説!←今回の記事. 因数分解の公式まとめ!それぞれのやり方は? 工夫して計算するやり方、2乗や小数をかんたんに! 式の計算の利用~円、正方形の図形の証明をイチから~ ★上級者向け★. 因数分解の難問を解説!. 3次以上の多項式の展開・因数分解の公式の総まとめ | 合格タクティクス. x 3 + y 3 + z 3 − 3 x y z の因数分解. 次の公式は3文字の因数分解公式ですが,よく問われるので知っておきたい公式です.. 実数 x, y, z に対して,次の等式が成り立つ.. 